Definition der mit dem Zugversuch ermittelten Werkstoff-Kenngrößen:

• Der Elastizitätsmodul (E) ist ein Maß für die Steifigkeit eines Werkstoffes und dem  Widerstand gegenüber der elastischen Verformung. Er ist ein Materialparameter, der bestimmt, wie sich ein Körper unter einer Zug- oder Druckkraft in Richtung der Kraft verformt
• Die Dehngrenze (R_p0,2) ist die Spannung bei einem bestimmten Betrag an bleibender (plastischer) Dehnung. Sie wird bei Werkstoffen mit allmählichem Übergang vom elastischen zum plastischen Werkstoffverhalten als Ersatz für die Streckgrenze verwendet.
• Die Streckgrenze (R_e) wird in MPa angegeben und ist die Spannung, bei der es zum Übergang von elastischen zur plastischen Verformung kommt. Sie ist der höchste Punkt, bis zu dem gedehnt werden kann und wieder in den Ausgangszustand zurück kehrt.
• Unter der Bruchdehnung (A) versteht man, die bleibende (plastische) Dehnung nach dem Bruch. Sie ist die Probenverlängerung nach dem Bruch bezogen auf di Ausgangsmesslänge in %.
• Einschnürung bzw. Brucheinschnürung: beim auseinander „ziehen“ der Zugproben ist meist eine Einschnürung (Verringerung des Probenquerschnitts) zu erkennen. Die Bruchdehnung (Z) ist die größte Querschnittsänderung der Zugprobe im Bereich der Einschnürung bezogen auf den Anfangsquerschnitt in %.
• Die Poissonsche Querkontraktionszahl ist der materialabhängige Proportionalitätsfaktor, der angibt, in welchem Verhältnis die Längsdehnung ε und die gleichzeitig eintretende Querkontraktion zueinander stehen, wenn ein Probekörper (z. B. Stab, Draht) elastisch auf Zug beansprucht wird.

Wie werden aus den im Zugversuch aufgenommenen Kraft-Verlängerungskurven Spannungs-Dehnungsdiagramme berechnet?
Um allgemeine Informationen über das Festigkeits- und Dehnungsverhalten eines Werkstoffs zu erhalten, wird aus einem Kraft-Verlängerungs-Diagramm ein Spannungs-Dehnungs-Diagramm entwickelt. Dazu wird mit Hilfe, der durch den Zugversuch ermittelten Werte, mit folgenden Formeln Spannungs- und Dehnungswerte errechnet und in einem Diagramm grafisch dargestellt.

Warum handelt es sich dabei um scheinbare Spannungs-Dehnungs-Diagramme?
Die beim Zugversuch wirkenden Kräfte werden stets auf den Ausgangsquerschnitt der Zugprobe bezogen, der in Wirklichkeit bei der Verlängerung der Zugprobe (z.B. Stab) kleiner wird.

Die wahre Spannung ist die momentane Kraft bezogen auf den momentanen Querschnitt. Der Werkstoff hat also eine höhere Festigkeit als aus dem Kraft-Verlängerungs-Diagramm abgelesen und somit errechnet werden kann.

Was ist das Hookesche Gesetz?
Es beschreibt das elastische Verhalten eines Körpers bzw. Werkstoffs. Mit zunehmender Spannung steigt die Dehnung, im Bereich der elastischen Verformung, linear an. Das bedeutet die elastische Verformung des Werkstoffs ist proportional zur auf die Probe wirkende Belastung.

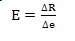
Meist ist in einem Spannungs-Dehnungs-Diagramm eine Linear steigende Gerade (Hook’sche Gerade) zu erkennen. Sie ist der geradlinige Bereich (Bereich der elastischen Verformung) am Anfang eines solchen Diagramms. Der Anstieg der Hook’schen Gerade ist für jeden Werkstoff charakteristisch und wird als Elastizitätsmodul E bezeichnet.

Vergleiche einiger Elastizitätsmodule verschiedener Werkstoffe

Werkstoff	Elastizitätsmodul in GPa
Diamant	1000
Wolfram	406
Aluminiumoxid (Al2O3)	300 – 380
Nickel	214
Stahl	190 – 214
Kupfer	124
Siliziumoxid (SiO2)	72
Aluminium	70
PET	2,8
Polycarbonat (PC)	2,3

Der Elastizitätsmodul gibt die Steigung der Hookeschen Geraden (Bereich der elastischen Verformung) im Spannungs-Dehnungs-Diagramm an. Je steiler die Hookesche Gerade ist, desto größer ist der E-Modul.

Diamant hat unter den angegebenen Werkstoffen den Größten E-Modul, es muss eine höhere Kraft aufgewendet werden, um eine im Verhältnis dazu gering Dehnung zu erreichen. PET und Polykarbonat hingegen haben einen niedrigen E-Modul und somit eine flachere Steigung der Hookeschen Geraden. Somit kann mit relativ geringer Kraft eine hohe Dehnung im elastischen Bereich erreicht werden.

Welche Vorstellungen existieren über die Ursachen der Ausbildung einer ausgeprägten Streckgrenze bei Stählen?
Bei einer ausgeprägten Streckgrenze kann in untere Streckgrenze R_eL und obere Streckgrenze R_eH unterschieden werden. Diese „Zick-Zack“-Erscheinung im Diagramm wird auch als Lüdersdehnung bezeichnet. Eine ausgeprägte Streckgrenze entsteht nur bei duktilen Werkstoffen wie (unlegiert bzw. niedrig legiert) Stahl. Dabei tritt oberhalb der Elastizitätsgrenz ein Spannungsabfall ein, obwohl sich der Werkstoff gleichzeitig deutlich plastisch verformt. Der erste deutliche Kraftabfall im Diagramm bzw. beim Zugversuch wird als obere Streckgrenze bezeichnet. Die untere Streckgrenze hingegen ist die kleinste Spannung im Fließbereich (Lüdersdehnung). Eine ausgeprägte Streckgrenze tritt durch Anlagerung von eingelagerten (interstitiell) Atomen wie Kohlenstoff- und Stickstoffatomen an den Versetzungen auf. Die Einlagerungsatome diffundieren in die Versetzungen und üben eine Druckspannung an diesen aus.

Eine Ursache für die Bildung einer ausgeprägten Streckgrenze ist z.B. das Vorhandensein von Gitterfehlern wie zum Beispiel Versetzungen. Diese Versetzungen ermöglichen eine plastische Verformung. Streckgrenzen mit einer Lüdersdehnung benötigen zusätzliche Energie zum zerreißen dieser Versetzungen. Danach nimmt die Zahl der gebildeten Versetzungen sprunghaft zu, so dass eine kleinere Spannung aufgewendet werden muss. Die Diffusion ist von der Temperatur beeinflussbar.